Learn Logic, Matty... Or Suffer The Wrath of Thy Interlocutors

Logic is not my forte. So prepare for a load of posts in which Matt tries to get to grips with stuff rather than declaring war on people I disagree with.

~~~

I suppose there's no particular reason not to kick off with the laws of thought, those three sexy rules that define for all and sundry what are valid inferences and what are not. Despite their name they are not about though per se, but logic. We're safe on that front.

Law of identity : F(x) ⊃ F(x)
Law of non-contradiction : ∼(p · ∼p)
Law of excluded middle : p ∨ ∼p

Britannica also mentions some exceptions re the excluded middle;

The law of excluded middle and certain related laws have been rejected by L.E.J. Brouwer, a Dutch mathematical intuitionist, and his school, who do not admit their use in mathematical proofs in which all members of an infinite class are involved. Brouwer would not accept, for example, the disjunction that either there occur ten successive 7’s somewhere in the decimal expansion of π or else not, since no proof is known of either alternative; but he would accept it if applied, for instance, to the first 10100 digits of the decimal, since these could in principle actually be computed.

James Danaher writes to terrific effect on the subject while also getting to grips with lots of the criticisms that various philosophers have raised about the applicability of these laws in certain contexts.

~~~

A quick key/legend is going to be needed here;

A B C are the Constants, so they are defined within some particular atomic proposition.

P Q R are the Variables, so they range across all atomic propositions within whatever greater proposition the budding logician is building.

φ ψ χ

are the Schematic Letters, so they range over all propositions ever!

See the trend outwards from ABC to

φ

ψ

χ

\neg means Negation or Denial, so that '

¬P' means 'not P'.

\land means Conjunction, so that 'P

∧ Q' means 'P and Q'. This leaves four combos where one or both are true, namely;

P is true and Q is true : P Q

P is true and Q is false : P ¬Q

P is false and Q is true : ¬P Q

P is false and Q is false : ¬P ¬Q

\lor means Disjunction, so that '

P ∨ Q' means 'P or Q'.

\to means Conditional, so that 'P

→ Q' means 'if P then Q'.
↔ means Biconditional, 'P ↔ Q' means 'P if and only if Q'.

In an act of shameless theft from Wikipedia I give you the...

... basic and Derived Argument Forms
Name	Sequent	Description
Modus Ponens	$((p \to q) \land p) \vdash q$	If $p$ then $q$ ; $p$ ; therefore $q$
Modus Tollens	$((p \to q) \land \neg q) \vdash \neg p$	If $p$ then $q$ ; not $q$ ; therefore not $p$
Hypothetical Syllogism	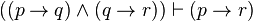$((p \to q) \land (q \to r)) \vdash (p \to r)$	If $p$ then $q$ ; if $q$ then $r$ ; therefore, if $p$ then $r$
Disjunctive Syllogism	$((p \lor q) \land \neg p) \vdash q$	Either $p$ or $q$ , or both; not $p$ ; therefore, $q$
Constructive Dilemma	$((p \to q) \land (r \to s) \land (p \lor r)) \vdash (q \lor s)$	If $p$ then $q$ ; and if $r$ then $s$ ; but $p$ or $r$ ; therefore $q$ or $s$
Destructive Dilemma	$((p \to q) \land (r \to s) \land(\neg q \lor \neg s)) \vdash (\neg p \lor \neg r)$	If $p$ then $q$ ; and if $r$ then $s$ ; but not $q$ or not $s$ ; therefore not $p$ or not $r$
Bidirectional Dilemma	$((p \to q) \land (r \to s) \land(p \lor \neg s)) \vdash (q \lor \neg r)$	If $p$ then $q$ ; and if $r$ then $s$ ; but $p$ or not $s$ ; therefore $q$ or not $r$
Simplification	$(p \land q) \vdash p$	$p$ and $q$ are true; therefore $p$ is true
Conjunction	$p, q \vdash (p \land q)$	$p$ and $q$ are true separately; therefore they are true conjointly
Addition	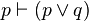$p \vdash (p \lor q)$	$p$ is true; therefore the disjunction ( $p$ or $q$ ) is true
Composition	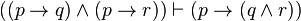$((p \to q) \land (p \to r)) \vdash (p \to (q \land r))$	If $p$ then $q$ ; and if $p$ then $r$ ; therefore if $p$ is true then $q$ and $r$ are true
De Morgan's Theorem (1)	$\neg (p \land q) \vdash (\neg p \lor \neg q)$	The negation of ( $p$ and $q$ ) is equiv. to (not $p$ or not $q$ )
De Morgan's Theorem (2)	$\neg (p \lor q) \vdash (\neg p \land \neg q)$	The negation of ( $p$ or $q$ ) is equiv. to (not $p$ and not $q$ )
Commutation (1)	$(p \lor q) \vdash (q \lor p)$	( $p$ or $q$ ) is equiv. to ( $q$ or $p$ )
Commutation (2)	$(p \land q) \vdash (q \land p)$	( $p$ and $q$ ) is equiv. to ( $q$ and $p$ )
Commutation (3)	$(p \leftrightarrow q) \vdash (q \leftrightarrow p)$	( $p$ is equiv. to $q$ ) is equiv. to ( $q$ is equiv. to $p$ )
Association (1)	$(p \lor (q \lor r)) \vdash ((p \lor q) \lor r)$	$p$ or ( $q$ or $r$ ) is equiv. to ( $p$ or $q$ ) or $r$
Association (2)	$(p \land (q \land r)) \vdash ((p \land q) \land r)$	$p$ and ( $q$ and $r$ ) is equiv. to ( $p$ and $q$ ) and $r$
Distribution (1)	$(p \land (q \lor r)) \vdash ((p \land q) \lor (p \land r))$	$p$ and ( $q$ or $r$ ) is equiv. to ( $p$ and $q$ ) or ( $p$ and $r$ )
Distribution (2)	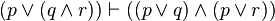$(p \lor (q \land r)) \vdash ((p \lor q) \land (p \lor r))$	$p$ or ( $q$ and $r$ ) is equiv. to ( $p$ or $q$ ) and ( $p$ or $r$ )
Double Negation	$p \vdash \neg \neg p$	$p$ is equivalent to the negation of not $p$
Transposition	$(p \to q) \vdash (\neg q \to \neg p)$	If $p$ then $q$ is equiv. to if not $q$ then not $p$
Material Implication	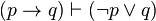$(p \to q) \vdash (\neg p \lor q)$	If $p$ then $q$ is equiv. to not $p$ or $q$
Material Equivalence (1)	$(p \leftrightarrow q) \vdash ((p \to q) \land (q \to p))$	( $p$ iff $q$ ) is equiv. to (if $p$ is true then $q$ is true) and (if $q$ is true then $p$ is true)
Material Equivalence (2)	$(p \leftrightarrow q) \vdash ((p \land q) \lor (\neg p \land \neg q))$	( $p$ iff $q$ ) is equiv. to either ( $p$ and $q$ are true) or (both $p$ and $q$ are false)
Material Equivalence (3)	$(p \leftrightarrow q) \vdash ((p \lor \neg q) \land (\neg p \lor q))$	( $p$ iff $q$ ) is equiv to., both ( $p$ or not $q$ is true) and (not $p$ or $q$ is true)
Exportation^[9]	$((p \land q) \to r) \vdash (p \to (q \to r))$	from (if $p$ and $q$ are true then $r$ is true) we can prove (if $q$ is true then $r$ is true, if $p$ is true)
Importation	$(p \to (q \to r)) \vdash ((p \land q) \to r)$	If $p$ then (if $q$ then $r$ ) is equivalent to if $p$ and $q$ then $r$
Tautology (1)	$p \vdash (p \lor p)$	$p$ is true is equiv. to $p$ is true or $p$ is true
Tautology (2)	$p \vdash (p \land p)$	$p$ is true is equiv. to $p$ is true and $p$ is true
Tertium non datur (Law of Excluded Middle)	$\vdash (p \lor \neg p)$	$p$ or not $p$ is true
Law of Non-Contradiction	$\vdash \neg (p \land \neg p)$	$p$ and not $p$ is false, is a true statement

Is A actually A? Well, using calculus you can do a chain of derivations - five of the suckers, referring to every step AFTER the premises - to sufficiently demonstrate the case, as below;

Number	Formula	Reason
1	$A$	premise
2	$A \lor A$	From (1) by disjunction introduction
3	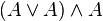$(A \lor A) \land A$	From (1) and (2) by conjunction introduction
4	$A$	From (3) by conjunction elimination
5	$A \vdash A$	Summary of (1) through (4)
6	$\vdash A \to A$	From (5) by conditional proof

That symbol that looks like a T knocked 90° anti-clockwise ( ⊢ ) means 'entails' or 'leads to' which is super useful;

$\vdash A$

can be then be read

I know $A$ is true".^[3]

In the same vein, a conditional assertion

$P \vdash Q$

can be read as:

From $P$ , I know that $Q$

Zeitardation

A Youtuber called axe863 made a video in which he used scientific, mathematical and statistical common-sense to deliver the KO that the Venus Project and Zeitgeist Movement so richly deserved. If his approach seems weird and unconventional it's because he's not attacking from a tradition neoclassical or Keynesian perspective. Axe863's poison is complexity economics, something a good deal more dangerous to ideas like TVP and TZM. [ 2 ] Now to a couple of comment threads from below the video that I thought could od with being replicated just in case they get deleted at source! ~~~ AstralLuminary 1 year ago Why can't we generalize the consumption patterns of middle-income people in the western world, set our constraints equal to the amount of localized resources, and the rate of resource recovery, derive a population growth model that would be sustainable to said consumption patterns, and derive the necessary quantifiable amount of work required to expen...

AynCrap

Search This Blog

Learn Logic, Matty... Or Suffer The Wrath of Thy Interlocutors

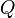
Comments

Post a Comment

Popular posts from this blog

Zeitardation

RIP Macroeconomics

Foreign Policy hates you...